Eftersom vi lever i popcorn-hjärnans era och dagens ungdom inte gärna läser saker över 140 tecken och dessutom inte är sådär jätteglada i naturkunskap överlag har jag fixat en liten länklista som leder till artikelns olika kapitel. Så slipper du som skyr ekvationer som pesten blunda när du scrollar. För the long story är det bara att bläddra neråt.

• Elo-rankingens grundprinciper (Helt fri från matematik, jag lovar!)
• Matematisk presentation av min modell
• Modellens världsranking
• Är modellen något att ha?
• Bonusstatistik

Vill också be om ursäkt till Albin Skur som fått utstå mången virriga meddelanden i inkorgen under arbetets gång. F’låt Hunkbin.

Bakgrund

Tanken att göra detta har funnits ett tag, men det var först när jag kollade upp världsrankingen inför VM 2016 som jag bestämde mig. I huvudsak går det att sammanfatta min motivation i en enda mening:

The IFF Rankings are based on the standings of the two previous WFC´s

Jäklar tänkte jag. Det är ju inte ens dåligt. Ren jävla lättja. Alla matcher utanför VM och VM-kval spelar således ingen som helst roll. Egentligen spelar inte heller matcherna någon roll då det enda som är viktigt är placeringen. Det är också helt omöjligt att sätta en siffra på hur mycket bättre ett lag är än ett annat. Det enda man kan utläsa av rankingen är exempelvis att Sverige för nuvarande är tre placeringar bättre än Danmark, vilket råkar vara lika mycket som USA har ner till Polen. Men jag vill påstå att det är förbannat många gånger mer sannolikt att Polen slår USA än att Danmark slår Sverige.

Så jag började fundera på hur det skulle gå att skapa ett bättre system för världsranking, som tog hänsyn till alla matcher men också kunde beskriva förhållandet mellan nummer 21 och 22 på listan på ett mer uttömmande vis än att det skiljer en placering på världsrankingen.

Och ganska snart snubblade jag över en herre som föddes i en stad som heter något så fantastiskt som Egyházaskesző.

Det ligger i nuvarande Ungern, och herren ifråga hette Élő Árpád Imre. Inte helt lätt att uttala det heller, men efter att han flyttat till USA som tioåring blev han något mindre tungvrickande Arpad Emmerich Elo. Han var professor i fysik på Marquette Universtity, och dessutom mästare på schack. Han gick lite i samma tankar som jag; hur ska man göra för att förbättra det befintliga rankingsystemet. Skillnaden mot mig är bland mycket annat att han har en professur i fysik, medan jag bara är en wannabe. Han fick saker gjorda. Och jag känner inte att jag behöver uppfinna hjulet igen. Så eftersom att hans rankingsystem fortfarande 60 år efter införandet används för att ranka schackspelare testade jag att anpassa det till internationell innebandy.

Grundläggande princip

Förenklat kan man säga att det är ett poängsystem där vinnaren tar poäng av förloraren. Alltså, varje spelare har en poäng, en Elo-rank. Magnus Carlsen har exempelvis 2840 i skrivande stund. När två spelare möts, exempelvis nyss nämnde Carlsen och hans närmaste utmanare, den gode Fabiano Caruana med sina 2823 poäng, ställs deras poäng mot varandra. Spelaren som vinner tar poäng av sin motståndare, men hur mycket beror på skillnaden i Elo-rank.

Eftersom Carlsen har högre poäng än Caruana ses det som mer sannolikt att det är han som kommer gå segrande ur partiet och att han slår Caruana är inte en lika stor bedrift som om Caruana slår Carlsen, och därmed ger en seger för Carlsen ett mindre antal poäng än vad Caruana fått om han hade vunnit. Blir det istället Remi (lika) tar den lägre rankade spelaren en liten summa från den med högre rank, men inte alls lika mycket som om spelaren istället hade vunnit. Hade Carlsen vunnit mot mig hade han inte fått några poäng alls, men hade jag slagit Carlsen hade jag fått en jäkla massa. Är du med?

Det fina med en sådan modell är att den är självutjämnande. En övervärderad spelare kommer åka på stora poängtapp och snabbt sjunka i rank, medan en undervärderad spelare kommer vinna stora poängsegrar och stiga i rank. Tills de har nått sin verkliga nivå. Precis som med alla statistiska modeller blir noggrannheten bättre och bättre ju mer data man petar in.

Detta system har anpassats till olika lagsporter tidigare, som exempelvis basket, baseball och fotboll, men med vissa modifikationer. Jag har lånat vissa bitar här och var för att försöka få till en algoritm som passar innebandyn så bra som möjligt. Jag vill dock igen rejält understryka att jag inte förtjänar någon som helst kredd för principen, det enda jag gjort är att mejsla fram en modell som fungerar någorlunda väl för innebandy.

Matematisk modell

OBS! Den matematiska modellen har modifierats något sedan den som beskrivs här nedan. Här kan du läsa om den nuvarande versionen.

Grunden vilar stadigt på den som Arpad Elo byggt, vilken i sin tur bygger på sannolikhetslärans fördärvade vanvett. Jag är inte så vidare värst hemma i det fältet ska erkännas, men jag ska försöka guida dig så gott jag kan genom den matematik som min modell bygger på.

Allt utgår från nedanstående, förhållandevis enkla, ekvation (som vi kan kalla för Ekvation 1). Denna beräknas efter varje match som nationen spelar för att få fram en ny Elo-rank.

Där:

• R_n är nationens nya rankingpoäng
• R_o är nationens gamla rankingpoäng
• P_h är det faktiska utfallet av matchen ur hemmalagets synvinkel
• P_p är det förväntade utfallet av matchen ur hemmalagets synvinkel
• F är en viktningsfaktor

R_n är alltså summan av den gamla rankingpoängen plus förändringen efter matchen, det vill säga differensen mellan faktiskt och förväntat utfall multiplicerat med viktningsfaktorn. R_o är således samma sak som lagets R_n efter deras förra match. R_o för respektive nations första match sätts i nuläget relativt godtyckligt.

Sverige och Finland börjar på en Elo-rank på 1700 medan Schweiz, Tjeckien, Norge och Danmark börjar på 1500. Georgien och Kroatien börjar på 1200 medan Indien och Iran börjar på 1000. Det enda som styr detta initiala värde är min magkänsla. Det är dock mycket enkelt att ändra detta värde till något som ligger närmre det verkliga värdet, men jag har inte brytt mig särskilt mycket då Elo-modeller är självreglerande. Lagen kommer förr eller senare hamna rätt.

P_h är det faktiska utfallet av matchen ur hemmalagets synvinkel enligt Tabell 1.

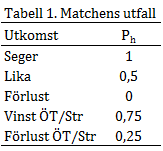
P_p är det förväntade utfallet av matchen ur hemmalagets synvinkel. Denna bestäms genom att jämföra lagens Elo-rank enligt Ekvation 2.

Där:

• R_h är hemmalagets Elo-rank innan matchen
• R_a är bortalagets Elo-rank innan matchen
• H är en parameter för hemmaplanfördel

R_h och R_a är således respektive lags R_o. Vid vänskapslandskamper (men inte vid turneringar och mästerskap) tillkommer också en parameter för hemmafördel. Jag har sett att hemmalaget vinner 55% av vänskapsmatcherna. Hemmalaget får då ett litet tillskott till deras Elo-rank om 35 poäng vilket korresponderar med en ökning på 5 %. Detta betyder sannolikheten att ett lag vinner över en helt jämlik motståndare i grunden är exakt 50 %, men tillskottet gör att sannolikheten klättrar upp till 55 %, alltså samma sannolikhet som det rent statistiskt är att hemmalaget vinner matchen.

För att åskådliggöra Ekvation 2 har jag i Figur 1 visat hur P_h förändras med differensen i Elo-rank mellan lagen.

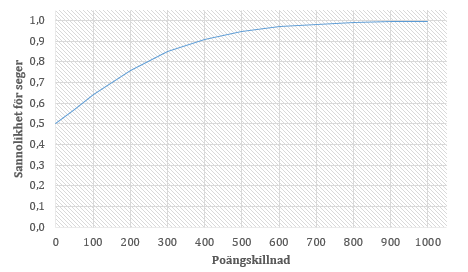
Figur 1: Sannolikheten för seger som funktion av skillnaden i Elo-rank

Såhär långt är det förhoppningsvis inte helt obegripligt, men nu ska vi blanda in en viktningsfaktor som är lite klurigare då den innehåller bökiga begrepp som naturlig logaritm, absolutvärde och Eulers tal. Ekvationen för att bestämma viktningsfaktor kan ses i Ekvation 3.

Där:

• K är hastighetsförändringen
• D är måldifferensen
• A är en faktor för autokorrelation
• e är Eulers tal

Schack är ganska binärt såtillvida att antingen vinner man eller förlorar man (eller spelar remi), och om man vinner så vinner man, om man förlorar så förlorar man. I innebandy är det stor skillnad på att vinna med 6-5 och vinna med 16-5, men att göra mål när man leder med 6-5 är ju väldigt mycket viktigare än att göra mål när man leder med 16-5. Av denna anledning logarimerar jag måldifferensen. F kan aldrig understiga 1.

Jag ville att min modell skulle klara av att ta hänsyn till såväl vinstmarginal som vilken typ av match det handlar om. Hastighetsförändringen K beror således på om det är en träningsmatch eller en mästerskapsturnering enligt Tabell 2.

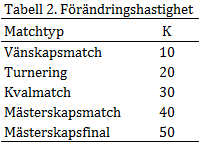
I praktiken medför detta att ju viktigare matchen är desto större utslag gör det för Elo-ranken.

Allt sammantaget går att åskådliggöra någorlunda i Figur 2, där viktningsfaktorn F skrivs som en funktion av vinstmarginalen D för olika fall av skillnad i Elo-rank. Figuren gäller enbart vid turneringsmatcher. Träningsmatcher kommer enligt Ekvation 3 och Tabell 2 alltså få ett lägre F än det som ses nedan medan en mästerskapsmatch tvärtom hade ökat F mot figuren nedan.

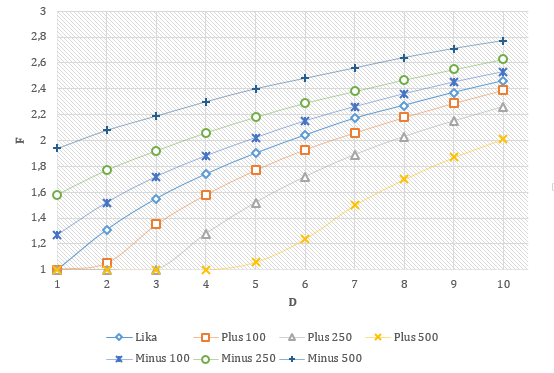
Figur 2. Viktningsfaktor som funktion av måldifferens och differens i Elo-rank

Om det lag som vinner har en Elo-rank 100 mer än motståndaren (Plus 100) innan matchen och vinstmarginalen är fyra mål medför det att F blir i runda slängar 1,6. Men om laget som vinner istället har 100 mindre än motståndarna (Minus 100) blir F ungefär 1,9. Vi kan också se att faktorn för måldifferens verkar enligt principen ”diminishing returns”. För att på något sätt ta i beaktande att innebandymatcher har en tendens att rinna iväg målmässigt är F konstruerad så att den inte blir 10 gånger större om ett lag vinner med 10 mål jämfört med 1 mål. Snarare blir den ungefär dubbelt så stor, exakt hur mycket beror på skillnaden i Elo-rank. Det kommer dock aldrig vara någon skillnad på 3-0 och 19-16 eftersom differensen är densamma.

Nu är jag fan klar.

Världsranking

Så, då har jag kommit fram till det viktiga: Min ranking. Men först en länk till Internationella Innebandyförbundets officiella ranking här.

Och här kommer motsvarande ranking för min modell. Vilken såklart visar alla nationers Elo-rank över tid.

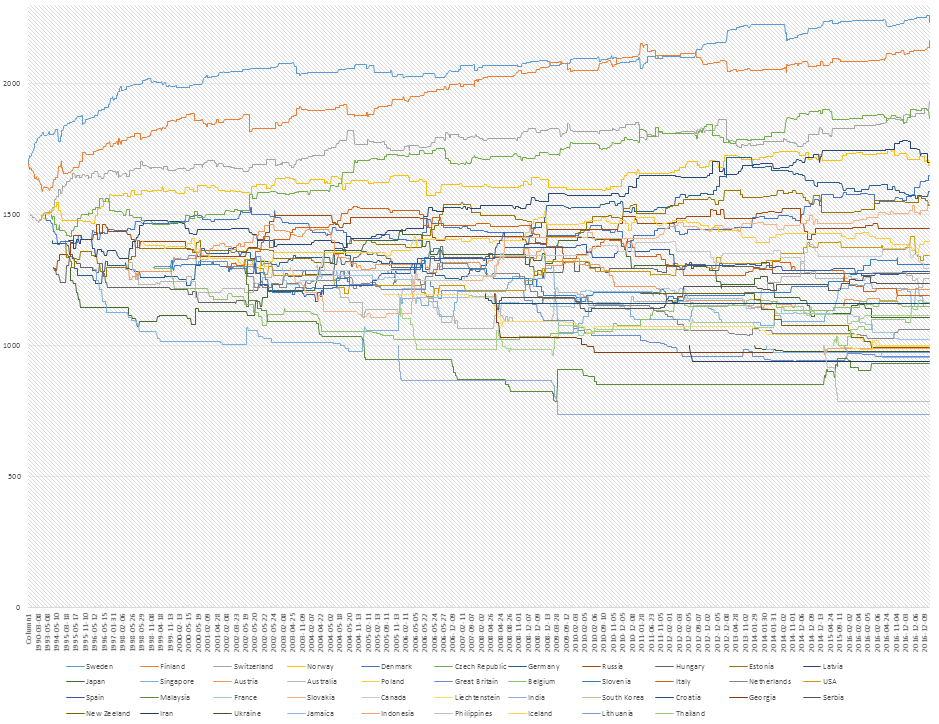
Det var kanske inte världens lättaste graf att läsa, så jag slänger upp nuvarande världsranking enligt min modell, med Elo-ranken i parentes.

Kom ihåg att en poängskillnad på 10 medför vinst i 51 % av fallen, poängskillnad på 100 medför vinst i 64% av fallen, 200 poängs skillnad medför vinst i 76 % av fallen och 500 poängs marginal medför vinst i 95 % av fallen. Enligt denna modell vinner Sverige mot Finland i 59 % av fallen, Schweiz i 85 % av fallen och Tjeckien i 89 % av fallen. Enligt statistiken vinner Sverige mot Finland i 61 % av fallen, mot Schweiz i 84 % av fallen och mot Tjeckien i 95 % av fallen. Måste säga att jag är ganska nöjd med den precisionen.

Är det ens någon mening?

Kort svar: Nej, skitstor skillnad är det inte. Det har dessutom tagit en jävla tid. Men å andra sidan tycker jag det är roligt att nörda ner mig i saker, speciellt statistik och innebandy. Och jag tycker faktiskt att innebandyvärlden förtjänar ett rankingsystem som är lite mer mångsidigt än det som finns idag. Det finns ju faktiskt några roliga grejer man kan göra med denna modell.

Exempelvis:

• De enda gånger det bäst rankade laget enligt min modell inte vunnit VM-guld var 2008 och 2016 och då gick matcherna till övertid. Kanske inte skitcoolt att pricka rätt på VM-segrare med 83 % sannolikhet, MEN:
• När Finland tog sitt historiska första VM-guld 2008 skilde futtiga 17 poäng inför matchen, och sannolikheten att Sverige skulle vinna var således 52 % mot Finlands 48 %. Matchen gick till förlängning där Finland vann. OCH:
• När Finland vann sitt andra VM-guld 2010 hade min modell Finland som knappa favoriter, 52/48.
• Modellen har rätt segrare i 78 % av mästerskapmatcherna och 82 % av alla matcher.

Men hur står modellen sig mot den officiella? Det är lite knepigt att avgöra, men om man tar de två senaste mästerskapen, VM 2014 och VM 2016 kan vi göra en liten jämförelse. Vid båda mästerskapen jämförs den officiella världsrankingen i VM-kvalet med modellens Elo-rank precis innan mästerskapet börjar. Jämförelsen görs genom att se över hur båda rankingsystemen placerar de tio främsta. För varje placering fel ges modellen en straffpoäng. Exempelvis hade min modell Lettland på plats 6 innan VM 2014, men Lettland slutade femma. Då får jag en straffpoäng. Minst antal straffpoäng vinner.

För VM 2014 prickar den officiella rankingen 3 länders slutliga placering; Sverige (1), Finland (2) och Estland (8). Totalt missar världsrankingen att få in Slovakien (12) och Danmark (14) på topp 10, och man får totalt 15 straffpoäng. För VM 2016 prickar världsrankingen hela sex länder; Schweiz (3), Tjeckien (4), Norge (6), Tyskland (7), Estland (8) och Slovakien (9). Man missar dock återigen Danmark (12) som hamnade på en fin femteplats. Totalt får man 14 straffpoäng.

För VM 2014 prickar min modell 5 länders slutliga placering; Sverige (1), Finland (2), Tjeckien (3), Schweiz (4) och Estland (8). Missar däremot Slovakien (11) som kommer tia. Totalt 8 straffpoäng. För VM 2016 prickar modellen 4 länders slutliga placering;  Schweiz (3), Tjeckien (4), Norge (6) och Tyskland (7), men får med alla topp 10-lagen för totalt 12 straffpoäng.

VM-tipset slutar alltså 20-29 till Elo-modellens favör.

Tiden får utröna om tendensen är något mer än en tendens.

Den största fördelen jag ser är att det finns ett mått för hur mycket bättre lagen är än varandra. Vi kan ta exemplet jag använde i inledningen då jag skrev att enligt IFF är Sverige (2) tre placeringar bättre än Danmark (5), vilket är lika mycket som USA (11) är före Polen (14). Men enligt min modell är Sverige (1) sex placeringar bättre än Danmark (7) och slår Danmark i 97 % av fallen medan Polen (12) är till och med bättre rankade än USA (13) och vinner i 57 % av fallen. Det är en jävla skillnad. Siffran är numera inte bara en placering, det är också ett mått.

Självklart finns det brister i modellen.

• Den tar inte hänsyn till lag som inte spelat på länge. Ungern har inte spelat en match sedan VM 2014 och det medför att siffrorna haltar en aning. Ryssland hade ett långt uppehåll på 2000-talet som ställde till rankingen. Hur modellen ska hantera brist på matchning är ett problem att lösa.
• De utomeuropeiska lagen tenderar att vara sämre rankade enligt min modell jämfört med den officiella, vilket jag dock tror är mer rätt, då många europeiska lag som inte klarar kvalet håller högre klass än de flesta asiatiska lag. Utomeuropeiska lag har lättare att komma till VM och det gynnar dem enligt den officiella algoritmen för ranking.
• Ingen hänsyn tas till träningsmatcher som spelas på neutral plan. Inte heller någon fördel av hemmaplan under mästerskap eller turneringar beaktas.
• Modellen beräknar också viktningsfaktorn, F, lite märkligt om laget som vinner har mycket högre rank än förloraren (>400). Då får vinnaren en högre faktor vid vinster med mindre än fyra måls differens än för vinster med mer än fyra måls differens. I praktiken betyder det inte så mycket för när ett så mycket bättre lag vinner får de ändå bara någon enstaka poäng och 1,4 gånger lite är inte mycket mer än 1,2 gånger lite, men det stör mig något enormt. Jag har inte hittat vad felet beror på ännu.
• Det går att tweaka saker som initialvärde och K för att få bättre precision.
• Modellen är fortfarande i prototypstadiet, så det existerar säkert tusentals brister som jag inte insett ännu.

Bonusstatistik

För den som tycker att det ovan är 2300 ord dravel kommer här något lite mer kondenserat.

• Världshistoriens första landskamp spelades 28/9 1985 mellan Sverige och Finland. Matchen slutade 12-1 till Sverige.
• Finland vann första gången mot Sverige på sitt fjärde försök. Matchen slutade 3-2.
• Sveriges har spelat 281 matcher, och på dessa tagit 722 poäng. Målskillnaden är 2356-734
• Finland har varit bättre än Sverige vid två tillfällen. Under korta perioder VM 2008 och 2010 som också slutade med VM-guld.
• Schweiz har släppt in flest mål av alla, 1206 stycken. Iran har gjort minst antal mål, 2 stycken.
• Den högsta Elo-ranken någonsin är 2260,3. Det var Sverige som slog rekordet efter semifinalen under VM i Riga.
• Indien har spelat 9 matcher, förlorat alla. Målskillnaden 6-334.
• Spanien har tredje bäst poängsnitt av alla, 1,74, jämfört med Sveriges 2,57 och Finlands 2,05.
• 8 landskamper har slutat 1-0. Tjeckien och Schweiz har mötts i tre av dem.
• Tjeckiens poängsnitt är 1,36 vilket räcker till en medför att man har länder som Österrike, Australien, Italien och Serbien framför sig.
• Thailand är det enda lag från Asien som har positiv målskillnad, 78-57.
• Nya Zeeland är det lag som spelat flest landskamper utan att ta en enda poäng, 12 stycken.
• Sverige har förlorat 23 landskamper. 22 mot Finland och 1 mot Tjeckien.
• Schweiz och Norge är de enda lag som förutom Finland och Tjeckien tagit poäng av Sverige. Schweiz tio gånger och Norge en.
• Japan har målrekordet i en landskamp. 59 stycken mot Indien. Då höll man också nollan.
• Den enda landskamp som slutat med tvåsiffrigt åt båda håll är Ungern – Slovenien som slutade 11-10 efter förlängning.
• Finland har spelat flest landskamper, 283 stycken.

Det var en liten del av vad som finns att hämta. Nu väntar jag bara på att IFF ska slå en pling.

Har du funderingar, tveka inte på att höra av dig till mig, antingen här nedan i kommentarsfältet, på twitter eller på mail.

Ha det gott