Detta inlägg är alltså en uppföljning till mitt försök att skapa ett nytt system för att ranka innebandylandslag. Du hittar det inlägget här. En uppmärksam läsare (tack Line!) kunde notera att ett fel letat sig in i Ekvation 2 som jag nu åtgärdat.  Den beräknade givetvis P_p (som i prediktion) och inte P_h (som i hemmalag) som jag skrivit tidigare. Jag inser också vid en ny titt att mina beteckningar kunde valts med lite större omsorg för att vara lite mer logiska så därför tänkte jag revidera dessa för att inte krångla till det i onödan. Försök glöm det jag skrev då och så tar vi nya tag idag. Mycket nya beteckningar jämfört med första versionen alltså. Nedan följer all nomenklatur som används, och vilken funktion dessa har gås igenom efter hand de används.

Nomenklatur

• α är en faktor för autokorrelation.
• D är måldifferensen ur hemmalagets synvinkel
• E_a är bortalagets Elo-poäng, inför matchen.
• E_h är hemmalagets Elo-poäng, inför matchen.
• E_n är den nya Elo-poängen, efter matchen.
• E_o är den gamla Elo-poängen, inför matchen.
• G är justering för måldifferensen.
• H är en justering för hemmaplansfördel, 35.
• K är en viktningsfaktor för matchens betydelse.
• R_h är matchens utfall ifrån hemmalagets synvinkel.
• R_p är matchens förmodade utfall ur hemmalagets synvinkel.

Matematisk beskrivning av modellen

Elo-systemet tar det tidigare värdet hos båda lagen och ändrar sedan dessa efter matchen beroende på resultatet i densamma enligt Ekvation 1:

Den beräknar hemmalagets nya Elo-poäng, E_n, genom att ta lagets Elo-poäng innan matchen, E_o, och sedan lägga på förändringen efter matchen, som alltså beror på saker som hur väntat resultatet, är, R_h-R_p, vilken typ av match det är, K, samt hur stor måldifferensen blev, G. Om laget inte spelat någon match än och därmed inte har något E_o används ett initialvärde. Här finns det två skolor.

Antingen får alla länder samma initialvärde och litar på att modellen fixar till eventuella fel. Fördelen med detta är att vi får ett konstant medelvärde. Om alla länder börjar på 1500 (vilket verkar vara praxis i Elo-kretsar) kommer medelvärdet för alla lag vara 1500 eftersom lagen tar poäng ifrån varandra i ett ”nollsumme-spel”, där vinnaren tar lika mycket som förloraren förlorar. Detta är ju trevligt då det är lätt att göra uppskattningar, och lätt att se hur bra ett lag är jämfört med alla andra. Nackdelen med att göra på detta sätt är ju att ett lag kan gå in på en nivå som är långt ifrån deras verkliga vilket gör att deras tidiga matcher kommer generera en missvisande poängsumma.

Det andra sättet är att ge länderna ett mer eller mindre godtyckligt initialvärde. Eventuellt kan man titta på lagets första tio matcher och sedan efterjustera för att pricka en nivå som ligger mer i linje med deras verkliga. På detta sätt kommer man ju omkring problemet med felaktiga resultat i början, men förlorar det stabila medelvärdet. Jag har gjort försök med båda och inte riktigt bestämt mig för hur jag ska göra. Det resultat jag redovisade igår var baserat på varierande initialvärden.

R_h redovisas i Tabell 1 nedan.

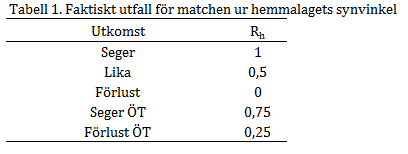
Sannolikheten för hemmaseger, Rp, beräknas med Ekvation 2.

H används i nuläget endast i träningslandskamper då modellen inte har något sätt att ta hänsyn till matcher på neutral mark (en sak som går att implementera relativt enkelt men som innebär en oerhört tidskrävande process att gå igenom samtliga 1721 landskamper och peta in ett värde. Det ska göras, men finns saker som går före i kön just nu). I träningslandskamper vinner hemmalaget i 55 % av fallen. 35 poäng läggs därför på hemmalagets Elo-poäng vilket innebär 5 % större sannolikhet för hemmaseger. Två jämnbra nationer som har 50/50 på neutral mark kommer alltså att ha 55/45 då matchen spelas i någon av länderna. I Figur 1 ses hur sannolikheten för vinst beror av skillnaden i Elo-poäng.

Faktorn som viktar matchens betydelse, K, kan egentligen tänkas bestå av två delar. Dels den som syns i Tabell 2 här nedan. Där ser vi alltså viktningsförhållandet som ska göra skillnad på match och match. Ett sömnigt dubbelmöte mot Norge i mars ska helt enkelt inte spela lika stor roll i rankingen som en semifinalseger. Hur det här inbördes förhållandet ska se ut är inte hugget i sten i nuläget, men nedanstående duger gott än så länge. Jag har sett 20 användas för fotboll och basket, 8 för ishockey och 4 för baseboll.

Men sedan finns där en osynlig komponent som styr hur trögt systemet i sin helhet är. Höga K-värden medför att ”minnet” är kort, vilket alltså betyder att nya matcher ger stort utslag. Höga K-värden är alltså ett sätt att säga att det finns mycket information att hämta i en match. Låga K-värden betyder såklart det motsatta; att den enskilda matchen inte spelar så stor roll, vilket gör att det är långsiktiga trender som är viktiga. Jämför  fotboll med baseboll och du ser att det finns mycket mer information i en fotbollsmatch än en basebollmatch. Att dessa värden hamnar på rätt nivå är såklart oerhört viktigt för om K-värdet är för högt kommer modellen att bli explosiv och ostadig, men om K-värdet är för lågt blir modellen för långsam och hinner inte plocka upp mer eller mindre tillfälliga formtoppar. Experimentering med K-värdet kommer definitivt vara en av de saker jag tittar på i framtiden.

Sedan har vi den sista komponenten i Ekvation 1: Justeringen för måldifferens, G, som kan ses i Ekvation 3.

Denna faktor används för göra skillnad på en 1-0 seger och en 10-0 seger och också jämföra med det förväntade resultatet. Skillnaden mellan den verkliga måldifferensen och den förväntade måldifferensen (ungefär 3,2 mål per 100 Elo-poäng skillnad) logaritmeras för att lite ta udden ur de matcher som rinner iväg. Det ska helt enkelt vara viktigare att gå från 3-2 till 4-2 än från 13-2 till 14-2. Om G understiger 1 kommer den ändå sättas till 1.

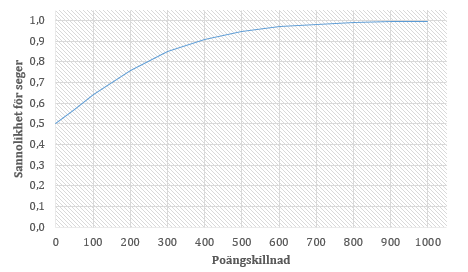
Det är enklare att se hur det fungerar i Figur 2 nedan.

Om det lag som vinner har 100 Elo-poäng än motståndaren (Plus 100) innan matchen och vinstmarginalen är fyra mål medför det att G blir i runda slängar 1,6. Men om laget som vinner istället har 100 mindre än motståndarna (Minus 100) blir G ungefär 1,9. Vi kan också se att faktorn för måldifferens verkar enligt principen ”diminishing returns”. För att på något sätt ta i beaktande att innebandymatcher har en tendens att rinna iväg målmässigt är G konstruerad så att den inte blir 10 gånger större om ett lag vinner med 10 mål jämfört med 1 mål. Snarare blir den ungefär dubbelt så stor, exakt hur mycket beror på skillnaden i Elo-rank. Det kommer dock aldrig vara någon skillnad på 3-0 och 19-16 eftersom differensen är densamma.

Exempel: Träningsmatch Slovakien – Lettland, 4-5

Exempelmatchen spelas mellan Slovakien och Lettland, där Slovakien står som hemmalag. E_o är den ingående Elo-poängen, vilken är 1491 för Slovakien och 1620 för Lettland. Skillnaden mellan lagen är 129 poäng. Eftersom matchen är en träningsmatch där Slovakien är hemmalag får Slovakien en hemmalagsbonus på 35 poäng och står därmed på 1526 poäng. Då är skillnaden 94 poäng.

När jag räknar utgår jag alltid från hemmalaget. Och när jag räknat ut hemmalagets E_n är det bara att dra bort samma siffra för att få bortalagets E_n eftersom det alltid är så att lagen tar poäng ifrån varandra. Det blir således aldrig mer poäng i omlopp, snittet är konstant.

Först räknas R_p ut enligt ekvation 2. Detta betyder alltså att Slovakien väntas vinna med 37 % sannolikhet om man spelar träningslandskamp mot Lettland. Om de båda möts i ett mästerskap är sannolikheten istället 32 %.

Vi använder ekvation 3 för att ta fram G.

Då har vi allt för att peta in i Ekvation 1.  R_h hämtas från Tabell 1 och eftersom Slovakien (hemmalaget) förlorade är R_h = 0. K hämtas från Tabell 2 och eftersom det är en träningsmatch är K = 10.

Slovakien får alltså en Elo-poäng på 1486 efter matchen, en minskning med 5 poäng. Lettland, som började på 1620 poäng får således 1625 efter matchen.

På samma sätt kan man räkna ut att om Slovakien vunnit med 5-4 hade man tagit 11 poäng av Lettland och stått på 1502 efter matchen medan Lettland skulle stå på 1609, detta eftersom att en seger är mer värd för det sämre rankade laget. Om Slovakien istället vunnit med 5-4 i ett VM hade man knyckt hela 52 poäng av Lettland, medan det varit 26 om det varit i en turnering. Om en turneringsmatch slutat lika hade Slovakien, som är det sämst rankade laget, tagit 6 poäng av Lettland. Det är just att Elo-ranken är så organisk som är dess storhet och det som gör att lagens poäng automatiskt kommer att gå mot deras verkliga nivå. Det handlar bara om att ta fram rätt faktorer för att få så precist resultat som möjligt.

Utvecklingen pågår, och tips mottages tacksamt, gärna på twitter eller på mail. Det går också bra att kommentera här nedan om du har några frågor, jag ska göra mitt bästa för att svara på dem. Innebandyns statistikrevolution har börjat!