En del av försnacket har handlat om det faktum att innebandyn inte kommer att spelas med innebandyregler i helgen. Från början var det till och med så att planen skulle vara en aning mindre än normalt, men det problemet har arrangörerna lyckats lösa. Väl det. Kvar är kortare speltid (3×15) och rejält bantade trupper (12+2 spelare). Jag tycker inte om det alls. Men så är jag otroligt gubbgrinigt lagd. Jag gillar inte att en extern instans går in och strömlinjeformar min sport för att passa i ett schema.

Tycker dock inte att det är så störande att det tar ut glädjen över att innebandyn äntligen fått ett erkännande av den olympiska familjen. Nu delar innebandyn visserligen scen med andra marginalidrotter som fensim, livräddning och korfball, men nog är det bättre än att vara utanför den gemenskapen som rossallhockey, armbrytning och i stort sett alla grenar i Nude Olympics är. Det är en bra start.

Jag kan ju inte hålla mig ifrån att prata Elo så jag måste tippa utgången av turneringen. Elo tippar ett par skillnader mot den officiella världsrankingen. Enligt Elo är Sverige, trots silvret i senaste VM, fortfarande rankat som bäst i världen. Dessutom är hemmafördelen tillräcklig för att Polen ska gå om USA.  Elo förutspår följande sluttabell (med officiella rankingen inom parentesen):

1. Sverige (2)
2. Finland (1)
3. Schweiz (3)
4. Tjeckien (4)
5. Polen (6)
6. USA (5)

Vinstchansen för respektive lag i gruppspelsmatcherna ses nedan:

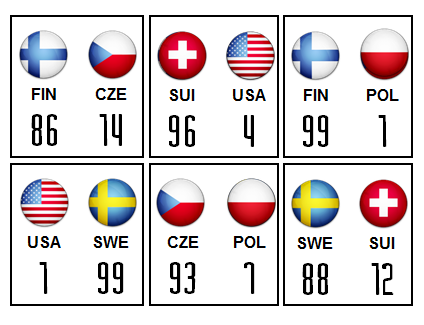
Känns som att det ska mycket till för att något lag ska skrälla i gruppspelet. För den riktigt nördige kan en omvandla procenten ovan till vinstmarginal (hänsyn tas till kortare speltid):

• Finland slår Tjeckien med 6 mål
• Schweiz slår USA med 10 mål
• Finland slår Polen med 12 mål
• Sverige slår USA med 14 mål
• Tjeckien slår Polen med 8 mål
• Sverige slår Schweiz med 6 mål

Känns inte helt och hållet rimligt, men vi får se hur det står sig. Det var allt jag tänkte ta idag. Har ju trots allt semester. Följ mig på twitter för fler och mer frekventa uppdateringar under helgen!